[논문리뷰] Entity Alignment between Knowledge Graphs Using Attribute Embeddings

• 해당 논문은 attribute (literal) embedding을 활용하여 두 개의 다른 지식 그래프를 하나의 공간 상에 매핑하는 프레임워크에 대해 연구하였다.

Abstract

The task of entity alignment between knowledge graphs aims to find entities in two knowledge graphs that represent the same real-world entity. Recently, embedding-based models are proposed for this task. Such models are built on top of a knowledge graph embedding model that learns entity embeddings to capture the semantic similarity between entities in the same knowledge graph. We propose to learn embeddings that can capture the similarity between entities in different knowledge graphs. Our proposed model helps align entities from different knowledge graphs, and hence enables the integration of multiple knowledge graphs. Our model exploits large numbers of attribute triples existing in the knowledge graphs and generates attribute character embeddings. The attribute character embedding shifts the entity embeddings from two knowledge graphs into the same space by computing the similarity between entities based on their attributes. We use a transitivity rule to further enrich the number of attributes of an entity to enhance the attribute character embedding. Experiments using real-world knowledge bases show that our proposed model achieves consistent improvements over the baseline models by over 50% in terms of hits@1 on the entity alignment task.

1 Introduction

• (Background) The same entity may exist in different forms in different KGs. → These KGs are complementary to each other in terms of completeness.
• To integrate KGs, a basic problem is to identify the entities in different KGs → This study focuses on entity alignment between two KGs.
• An RDF triple used in this study consists of three elements:
  • subject: entity
  • object: 1) entity (relationship triple), 2) letters (attribute triple).
  • relationship/predicate
• (Early studies) entity alignment: similarity between attributes of entities
  • 1) user-defined rules to determine the attributes to be compared between the entities
    • limitation: different pairs of entities may need different attributes to be compared
  • 2) embedding-based models to capture the semantic similarity between entities based on relationshup triples (e.g. TransE)
    • limitation: seed alignments between two KGs are rarely available, hence are difficult to obtain due to expensive human efforts required.
• (In this study) proposes a novel embedding model that 1) generated attribute embeddings from the attribute triples, 2) use attribute embeddings to shift the entity embeddings of two KGs to the same vector space.
  • 1) attribute similarity between two KGs helps the attribute embedding to yield a unified embedding space for two KGs.

  • 2) use the attribute embeddings to shift the entity embeddings of two KGs into the same vector space

    → the entity embeddings can capture the similarity between entities from two KGs.

  • also includes predicate alignment by renaming the predicates of two KGs into a unified naming scheme to ensure that the relationship embeddings of two KGs are also in the same vector space.
• (Contributions)
  • propose a framework for entity alignment between two KGs that consists of a predicate alignment module, an embedding learning module, and an entity alignment module.
  • propose a novel embedding model that integrates entity embeddings with attribute embeddings to learn a unified embedding space for two KGs
  • For over three real KG pairs, the model outperforms the state-of-the-art models consistently on the entity alignment task by over 50% in terms of hits@1

2 Related Work

2.1. String-Similarity-based Entity Alignment

1. use string similarity as main alignment tool
   1. LIMES (Ngomo and Auer 2011)
   2. RDF-AI (Scharffe, Yanbin, and Zhou 2009)
   3. SILK (Volz et al., 2009)
2. use graph similarity to improve performance
   1. LD-Mapper (Raimond, Sutton, and Sandler 2008)
   2. RuleMiner (Niu et al. 2012)
   3. HolisticEM (Pershina, Yakout, and Chakrabarti 2015)

2.2. Embedding-based Entity Alignment

[KG completion]

1. translation based KGE models
   1. distributed representation that separate the relationship vector space from entity vector space: TransE (Bordes et al. 2013), TransH (Wang et al. 2014), TransR (Lin et al. 2015), and TransD (Ji et al. 2015), …
   2. additional information along with the relationship triples to compute entity embeddings: DKRL (Xie et al. 2016), TEKE (Wang and Li 2016)
2. non-translation based KGE models
   1. tensor-based factorization and representating relationships with matrices: RESCAL (Nickel, Tresp, and Kriegel 2012) and HolE (Nickel, Rosasco, and Poggio 2016)
   2. bilinear tensor operator to represent each relationship and jointly models head and tail entity embeddings: NTN (Socher et al. 2013)
      • preserve the structural information of the entities: entities that share similar neighbor structures in the KG should have a close representation in the embedding space.

[Entity alignment]

1. Chen et al. (2017a; 2017b):
2. Zhu et al. (2017):
3. Sun, H, and Li (2017):

3 Preliminary

• A KG G consists of a combination of
  • relationship triples in the form of ⟨h, r, t⟩, where r is a relationship (predicate) between two entities h (subject) and t (object)
  • attribute triples in the form of ⟨h, r, a⟩ where a is an attribute value of entity h with respect to the predicate (relationship) r.
• Given two KGs G1 and G2, the task of entity alignment aims to find every pair ⟨h1, h2⟩ where h1 ∈ G1, h2 ∈ G2, and h1 and h2 represent the same real-world entity.
• We use an embedding-based model that assigns a continuous representation for each element of a triple in the forms of ⟨h, r, t⟩ and ⟨h, r, a⟩, where the bold-face letters denote the vector representations of the corresponding element.

3.1. TransE

• $

  h+r-t

  \approx0$

• $L=\sum_{(h,r,t) \in S}\sum_{(h’,r’,t’ \in S’)[r+d(h+r,t)-d(h’+r’-t’)]}$
• (Advantages) capture the semantic similarity between entities in the embedding space
• (Limitations) the entity embeddings computed on different KGs may fall in different spaces, where similarity cannot be computed directly.
  • Transition matrix to map the embedding spaces of different KGs into the same space (in existing studies) requires manually collecting a seed set of aligned entities from the different KGs to create the transition matrix, which do not scale and are vulnerable to the quality of the selected seed aligned entities.

4 Proposed Model

4.1. Solution Overview

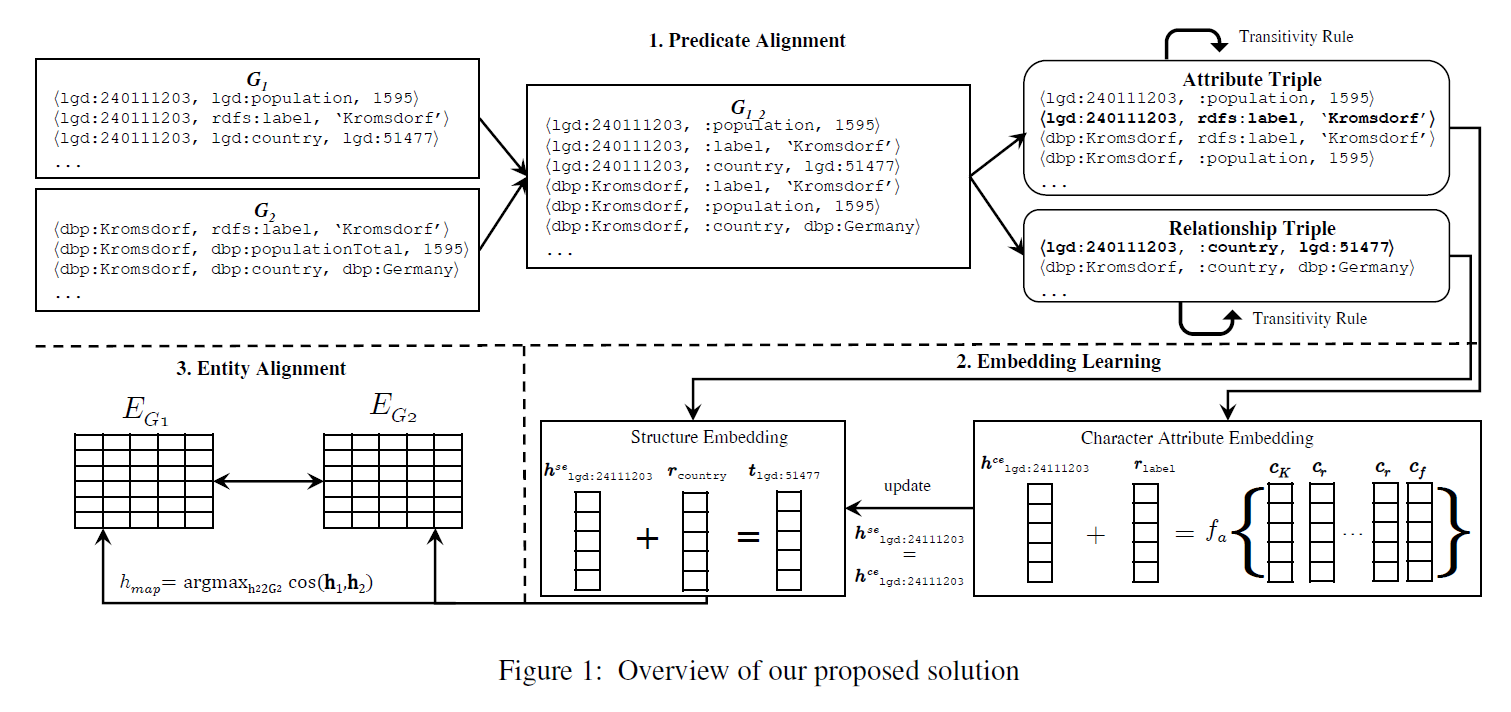
• Framework consists of three components: 1) predicate alignment, 2) embedding learning, and 3) entity alignment
• (requirement) relationship embeddings and entity embeddings of two KGs to fall in the same vector space
• (detailed in Section 4.2) To have a unified vector space for the relationship embeddings, we merge two KGs based on the predicate similarity (i.e., predicate alignment).
  • 1) The predicate alignment module finds partially similar predicates, and renames them with a unified naming scheme.
  • 2) Based on this unified naming scheme, we merge G1 and G2 into G1_2.
  • 3) Then, the merged graph G1_2 is split into a set of relationship triples $T_r$ and a set of attribute triples $T_a$ for embedding learning.
• (detailed in Section 4.3) The embedding learning module jointly learns the entity embeddings of two KGs using structure embedding and attribute embedding.
  • 1) The structure embedding is learned using the set of relationship triples $T_r$, while the attribute embedding is learned using the set of attribute triples $T_a$.
    • Initially, the structure embeddings of the entities that come from G1 and G2 fall into different vector spaces because the entities from both KGs are represented using different naming schemes.
    • In contrary, the attribute embeddings learned from the attribute triples $T_a$ can fall into the same vector space. This is achieved by learning character embeddings from the attribute strings, which can be similar even if the attributes are from different KGs (we call it as attribute character embedding).
  • 2) Then, we use the resulting attribute character embedding to shift the structure embeddings of the entities into the same vector space which enables the entity embeddings to capture the similarity between entities from two KGs.
• (detailed in Section 4.4) Once we have the embeddings for all entities in G1 and G2, the entity alignment module finds every pair ⟨h1, h2⟩ where h1 ∈ G1 and h2 ∈ G2 with a similarity score above a threshold β.
• (detailed in Section 4.5) To further improve the performance of the model, we use the relationship transitivity rule to enrich the attributes of an entity that helps build a more robust attribute embedding for computing the similarity between entities.

4.2. Predicate Alignment

• merges two KGs by renaming the predicates of both KGs with a unified naming scheme to have a unified vector space for the relationship embeddings.
  • To find the partially matched predicates, we compute the edit distance of the last part of the predicate URI (e.g., bornIn vs. wasBornIn) and set 0.95 as the similarity threshold.

4.3. Embedding Learning

• Aligning predicates of two KGs allows our model to have a unified relationship vector space and hence enables the joint learning of structure embedding and attribute character embedding that aims to yield a unified entity vector space.

1. Structure Embedding
   • adapt TransE to learn the structure embedding for entity alignment between KGs by focusing the embedding learning more on the aligned triples.
   • minimize the following objective function $J_{SE}$:
     • \[J_{SE}=\sum_{t_r \in T_R}\sum_{t'_r \in T_r'}max(0,\gamma+\alpha(f(t_r)-f(t_r'))), \alpha=\frac{count(r)}{|T|}\]
     • where \(T_r\): the set of valid relationship triples, \(T_r'\): corrupted relationship triples, $α$: a weight to control the embedding learning over the triples, \(count(r)\): number of occurences of relationship r, \(|T|\): total number of triples in KG \(G_{1\_2}\).
2. Attribute Character Embedding
   • Following TransE, for the attribute character embedding, we interpret predicate r as a translation from the head entity h to the attribute a.
   • 1) use a compositional function to encode the attribute value and define the relationship of each element in an attribute triple as $h + r ≈ f_a(a)$.
     • $f_a(a)$ is a compositional function and $a = {c_1, c_2, …, c_t}$ (sequence of the characters of the attribute value).
     • 1) Sum compositional function: $f_a(a) = c_1 + c_2 + c_3 + … + c_t$ → simple but cannot discriminate two strings with same characters and different orders
     • 2) LSTM-based compositional function: $f_a(a) = f_{lstm}(c_1, c_2, c_3, …, c_t)$ → use final hidden state of LSTM
     • 3) N-gram-based compositional function: \(f_a(a)=\sum_{n=1}^N(\sum^t_{i=1}\frac{\sum^n_{j=1}c_j}{t-i-1})\) where N: maximum value of n in n-gram → summation of n-gram combination
   • 2) minimize objective function \(J_{CE} = Σ_{t_a∈T_a}Σ_{t_a'∈T_a'}max (0, [γ + α (f(t_a) − f(t_a'))]) \\ T_a = \{⟨h, r, a⟩ ∈ G\}; f(t_a) = ∥h + r − f_a(a)∥ \\ T_a' = \{⟨h', r, a⟩| h' ∈ E\} ∪ \{⟨h, r, a'⟩ |a' ∈ A\}\)
     • where A: the set of attributes in G, $T’_a$: corrupted attribute triples (used as negative samples), $f(t_a)$: plausibility score based on embeddings of h and r, and the vector representation of the attribute value computed by $f_a(a)$
3. Joint Learning of Structure Embedding and Attribute Character Embedding
   • use the attribute character embedding $h_{ce}$ to shift the structure embedding $h_{se}$ into the same vector space by minimizing the following objective function:
     • $J_{SIM} = Σ_{h∈G_1∪G_2}[1 − cos(h_{se}, h_{ce})]$ where cos: cosine similarity
   • the structure embedding captures the similarity of entities between two KGs based on entity relationship while the attribute character embedding captures the similarity of entities based on attribute values.

\[J=J_{SE}+J_{CE}+J_{SIM}\]

4.4 Entity Alignment

• The joint learning of structure embedding and attribute character embedding lets the similar entities from $G_1$ and $G_2$ to have a similar embeddings. Hence, the resulting embeddings can be used for entity alignment.
• $h_{map}=\arg\max_{h_2∈G_2}cos(h_1, h_2)$
  • $⟨h_1, h_{map}⟩$ is the expected pair of aligned entities
  • use a similarity threshold β to filter the pair entities that are too dissimilar to be aligned.

4.5. Triple Enrichment via Transitivity Rule

• Even though the structure embedding implicitly learns the relationship transitive information, the explicit inclusion of this information increases the number of attributes and related entities for each entity which helps identify the similarity between entities.
• We treat the one-hop transitive relation as follows.
  • Given transitive triples ⟨h1, r1, t⟩ and ⟨t, r2, t2⟩, we interpret r1.r2 as a relation from head entity h1 to tail entity t2. Therefore, the relationship between these transitive triples is defined as $h_1 + (r_1.r_2) ≈ t_2$.
  • The objective functions of the transitivity-enhanced embedding models are adapted from the $J_{SE}$ and $J_{CE}$ by replacing the relationship vector r with r1.r2.

5 Experiments

• Databases: DBpedia (DBP) (Lehmann et al. 2015), LinkedGeoData (LGD) (Stadler et al. 2012), Geonames (GEO)2, and YAGO (Hoffart et al. 2013)
  • We compare the aligned entities found by our model with those in three ground truth datasets, DBP-LGD, DBPGEO, and DBP-YAGO, which contain aligned entities3 between DBP and LGD, GEO, and YAGO, respectively.

  

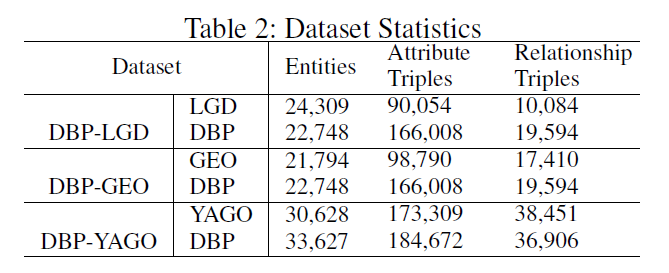
• Models: We use grid search to find the best hyperparameters for the models. We choose the embeddings dimensionality d among {50, 75, 100, 200}, the learning rate of the Adam optimizer among {0.001, 0.01, 0.1}, and the margin γ among {1, 5, 10}.We train the models with a batch size of 100 and a maximum of 400 epochs. We compare our proposed model with TransE (Bordes et al. 2013), MTransE (Chen et al. 2017a), and JAPE (Sun, Hu, and Li 2017).

5.1. Entity Alignment Results

• (Evaluation Methods) We evaluate the performance of the models using hits@k(k = 1, 10) (i.e., the proportion of correctly aligned entities ranked in the top k predictions), and the mean of the rank (MR) of the correct (i.e., matching) entity. Higher hits@k and lower MR indicate better performance.
• (Model Comparison) TransE: its embeddings of different KGs fall into different vector spaces → fails to capture the entity similarity between KGs
  • MTransE and JAPE: rely on the number of the seed alignments (we use 30% of the gold standard as the seed alignments as suggested in the original papers).

  

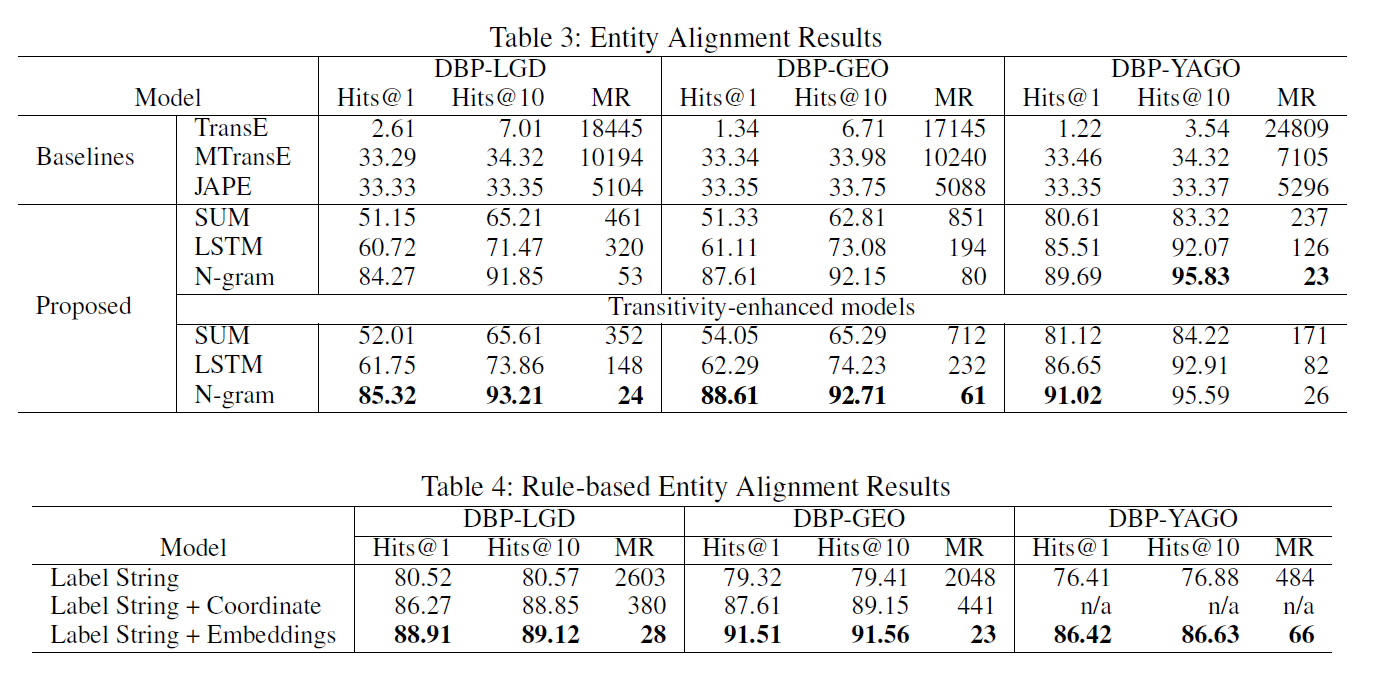
• (Compositional function) using the N-gram compositional function achieves better performance
  • since it preserves string similarity better when mapping attribute strings to their vector representations than the other functions.
• (Transitivity rule) improves the performance of the model since it enriches the attributes of the entities which allows more attributes to be used in the alignment.

5.2. Discussion

• (KG completion tasks) link prediction, triple classification

  

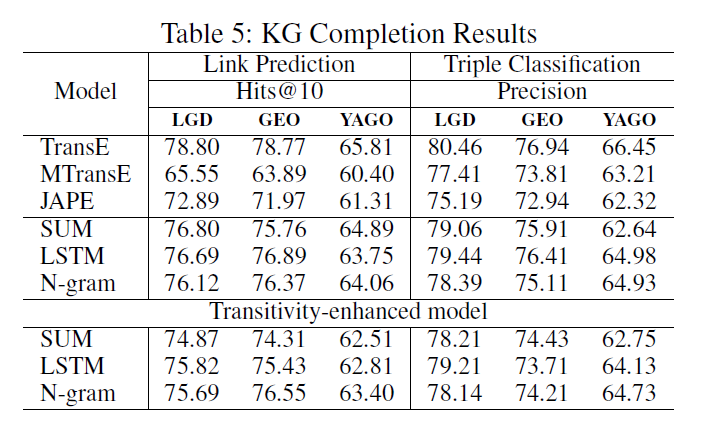
• (Link prediction) 1) each relationship triple is corrupted by replacing its head or tail with all possible entities in the dataset. 2) these corrupted triples are ranked ascendingly based on the plausibility score (h + r − t) (i.e., valid triples should have smaller plausibility scores than corrupted triples).
• (Triple classification) determine whether a triple ⟨h, r, t⟩ is a valid relationship triple or not. A binary classifier is trained based on the plausibility score (h + r − t).

6 Conclusion

• We proposed an embedding model that integrates entity structure embedding with attribute character embedding for entity alignment between knowledge graphs. Our proposed model uses the attribute character embedding to shift the entity embeddings from different KGs to the same vector space. Moreover, we adopt the transitivity rule to enrich the number of attributes of an entity that helps identify the similarity between entities based on the attribute embeddings. Our proposed model outperforms the baselines consistently by over 50% in terms of hits@1 on alignment of entities between three pairs of real-world knowledge graphs.

---

Framework 요약

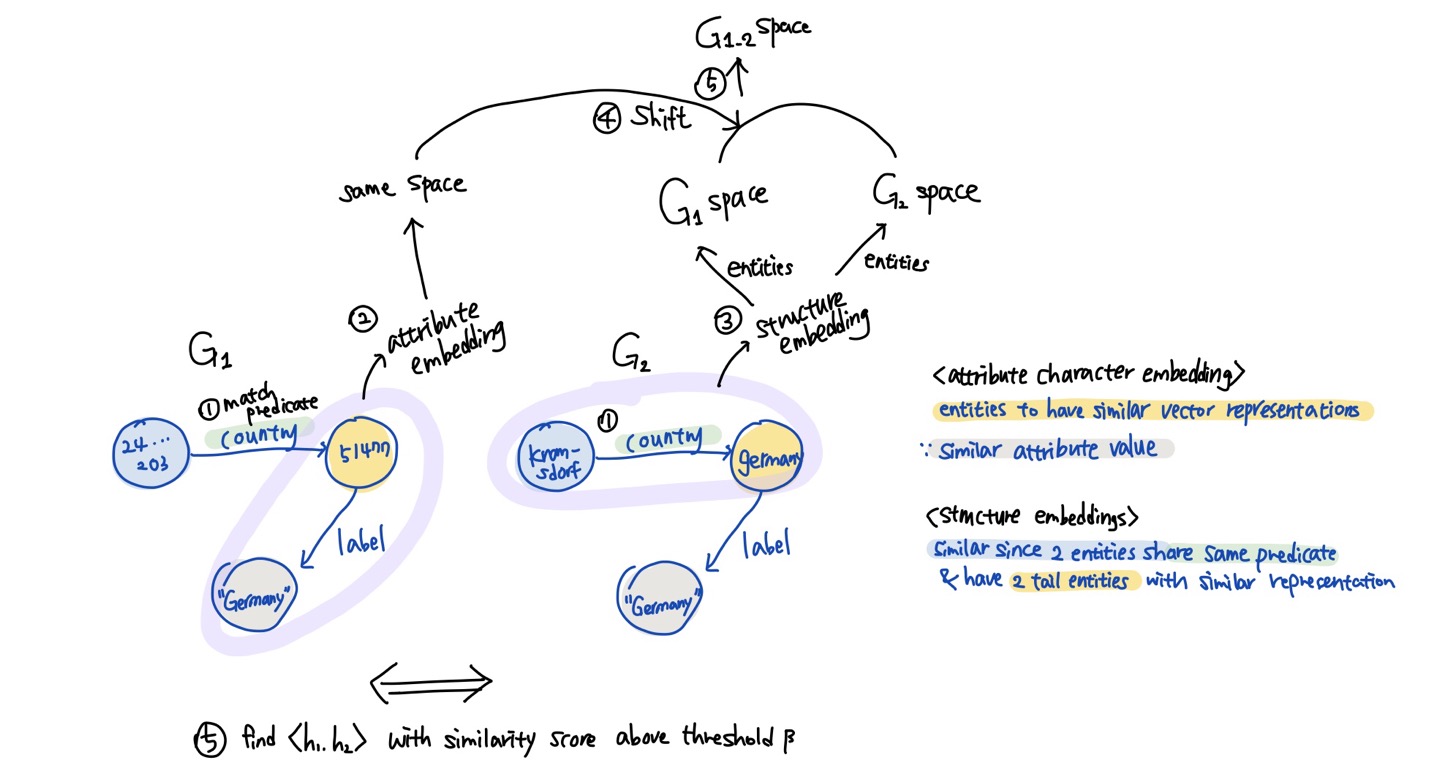
1. 두 지식 그래프에서 attribute 링크(predicate)에 대한 정보를 통일 (predicte alignment)
   • transivity rule (링크의 연속)을 사용하면 향후 similarity 정보를 더 잘 파악할 수 있음
2. structure embedding과 attribute character embedding 수행
   • structure embedding: TransE에 기반하여 embedding
   • attribute character embedding: letter 단위로 쪼갠 후 이를 composite 할 수 있는 세 가지 방법 제시 (sum, LSTM, n-gram)
   • joint learning: attribute embedding을 기준으로 하여 structure embedding을 같은 공간에 표현 (cosine similarity 기반) — 두 지식 그래프에 모두 적용하여 두 그래프 상의 유사한 entity는 유사한 embedding을 갖도록 (G1_node — attribute — G2_node 처럼)
3. Entity alignment
   • 다른 지식 그래프에 있는 node embedding과의 cosine similarity를 산출
   • 일정 threshold를 넘는 pair에 대해 align

---

• 해당 정리는 Notion에서도 확인하실 수 있습니다.