[논문리뷰] KGAT: Knowledge Graph Attention Network for Recommendation

• 해당 논문은 Knowledge graph based recommendation에 Attention을 적용하여 high-order connectivity에 대한 해석을 제공하였다.

Abstract

To provide more accurate, diverse, and explainable recommendation, it is compulsory to go beyond modeling user-item interactions and take side information into account. Traditional methods like factorization machine (FM) cast it as a supervised learning problem, which assumes each interaction as an independent instance with side information encoded. Due to the overlook of the relations among instances or items (e.g., the director of a movie is also an actor of another movie), these methods are insufficient to distill the collaborative signal from the collective behaviors of users.

In this work, we investigate the utility of knowledge graph (KG), which breaks down the independent interaction assumption by linking items with their attributes. We argue that in such a hybrid structure of KG and user-item graph, high-order relations— which connect two items with one or multiple linked attributes— are an essential factor for successful recommendation. We propose a new method named Knowledge Graph Attention Network (KGAT) which explicitly models the high-order connectivities in KG in an end-to-end fashion. It recursively propagates the embeddings from a node’s neighbors (which can be users, items, or attributes) to refine the node’s embedding, and employs an attention mechanism to discriminate the importance of the neighbors. Our KGAT is conceptually advantageous to existing KG-based recommendation methods, which either exploit high-order relations by extracting paths or implicitly modeling them with regularization. Empirical results on three public benchmarks show that KGAT significantly outperforms state-of-the-art methods like Neural FM and RippleNet. Further studies verify the efficacy of embedding propagation for high-order relation modeling and the interpretability benefits brought by the attention mechanism.

1 Introduction

• (Prior studies) User preference를 예측하기 위해 기존 연구들에서는 collaborative filtering (CF)와 supervised learning (SL)를 사용해왔음
  • CF: histories of similar users
    • side information을 고려하지 못함 → user-item의 관계가 sparse한 경우 성능 저하
  • SL: similar items with similar attribute
    • e.g. factorization machine (FM), neural FM (NFM), Wide&Deep, xDeepFM, …
    • 다양한 정보를 통합하고 high-order relation을 설명할 수 있으나 각 interaction을 독립적으로 판단하여 그들 간의 관계를 고려하지 못함

• (Collaborative Knowledge Graph) SL의 단점을 보완하고자 지식 그래프 구조와 user-item graph를 결합한 collaborative knowledge graph (CKG)를 정의, CKG를 활용하여 추천 방법 제안

  

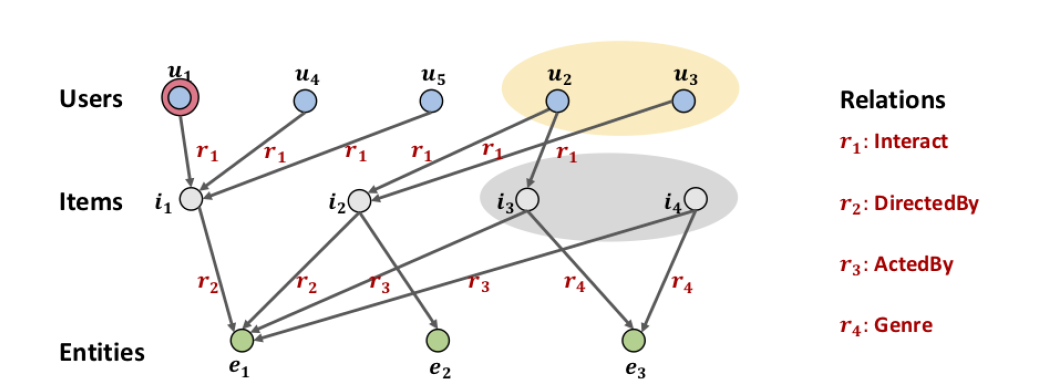
  • (challenges) to exploit high-order information: 1) computational overload (order의 차원이 증가하면 고려해야할 nodes가 dramatically 증가), 2) relation의 weight을 잘 결정해야 함 (high-order relations가 prediction에 있어 다르게 contribute)
• previous studies on CKG
  • path-based methods: 1) apply path selection algorithm to select prominent paths OR 2) define meta-path patterns to constrain the paths
    • 1)의 경우 처음 선택되는 path가 결과에 큰 영향을 끼칠 수 있으며 2)의 경우 도메인 지식을 필요로 함
  • regularization-based method: loss term을 사용하여 KG structure을 구성 (e.g. KTUP, CFKG)
    • implicit하게 그래프를 encode하므로, long-range connectivity를 잘 capture하는지 확신할 수 없고, 결과에 대해 해석할 수 없음
• (In this study) Knowledge Graph Attention Network (KGAT)를 제안
  • high-order relation modeling
    • 1) recursive embedding propagation: 이웃 노드들의 임베딩을 반영하여 타겟 노드의 임베딩을 업데이트, 이 방식을 반복하여 high-order connectivities를 capture
    • 2) attention-based aggregation: attention을 사용하여 각 이웃 노드의 weight을 학습, 중요도 파악
  • 기존 모델들에 비교하여 KGAT의 장점
    • 1) path-based methods에서 각 path를 구체화(materialize)할 때 드는 labor-intensive process가 없음
    • 2) regularization-based methods과 달리, high-order relation에 대한 정보를 바로 사용하므로 long-range connectivity가 반영됨
  • Contributions
    • We highlight the importance of explicitly modeling the high-order relations in collaborative knowledge graph to provide better recommendation with item side information.
    • We develop a new method KGAT, which achieves high-order relation modeling in an explicit and end-to-end manner under the graph neural network framework.
    • We conduct extensive experiments on three public benchmarks, demonstrating the effectiveness of KGAT and its interpretability in understanding the importance of high-order relations.

2 Task Formulation

• (User-Item Bipartite Graph) user-item interation; $G_1= {(u,y_{ui} , i)|u ∈ \mathcal{U}, i ∈ \mathcal{I})}$, where $\mathcal{U}$ and $\mathcal{I}$ separately denote the user and item sets, and a link $y_{ui} = 1$ indicates that there is an observed interaction between user u and item i; otherwise $y_{ui} = 0$.

• (Knowledge Graph) side information; $G_2= {(h, r , t )|h, t ∈ \mathcal{E}, r ∈ \mathcal{R}}$, $\mathcal{R}$: relation (canoncial & inverse), $A = {(i, e)|i ∈ \mathcal{I}, e ∈ \mathcal{E}}$

• (Collaborative Knowledge Graph) $G = {(h, r , t )|h, t ∈ \mathcal{E}’, r ∈\mathcal{R}’}$ , where $\mathcal{E}’ = \mathcal{E} ∪\mathcal{U}$ and $\mathcal{R}’ = \mathcal{R} ∪ {Interact}$.

• (Task Description)
  • Input: collaborative knowledge graph (user-item bipartite grpah + knowledge graph)
  • Output: prediction function (user u가 item i를 adopt할 확률)
• (High-Order Connectivity) L-order connectivity: $e_0 \xrightarrow{r_1} e_1 \xrightarrow{r_2} \cdots \xrightarrow{r_L}e_L$ , where $e_l \in \mathcal{E}’, r_l \in \mathcal{R}’, (e_{l-1}, r_l, e_l)$: l-th triplet, L: length of the sequence

3 Methodology

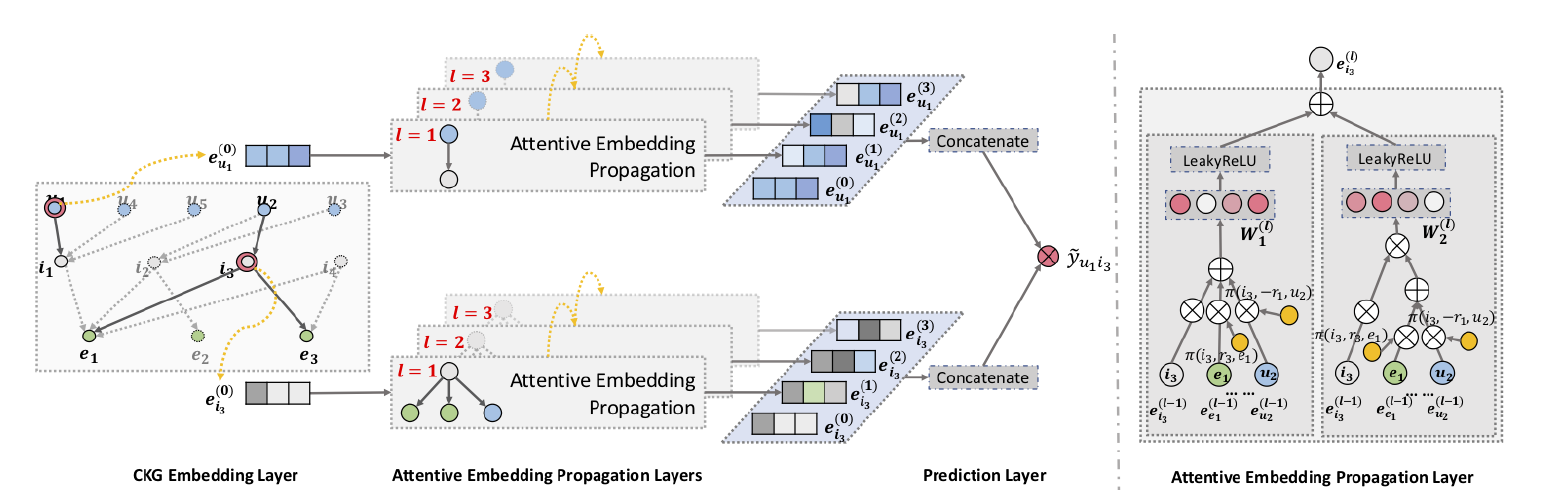
• Components
  • 1) embedding layer: CKG에 기반하여 node를 vector로 임베딩
  • 2) attentive embedding propagation layers: 주위의 node 정보를 받아 임베딩을 propagate (반복 update + attention)
  • 3) prediction layer: matching score를 예측

3.1. Embedding Layer

• TransR을 기반으로 임베딩
  • translation principle $e^r_h+e_r ≈ e^r_t$을 만족하도록 entity와 relation을 임베딩
  • $e^r_h, e^r_t$는 $e_r$ 공간 상에 각각 $e_h, e_t$으로 표현됨 ($e_h, e_t \in \mathbb{R}^d, e_r \in \mathbb{R}^k$)
  • plausibility score: $g(h, r , t ) = ∥W_r e_h + e_r −W_r e_t ∥^2_2$, $W_r \in \mathbb{R}^{k \times d}$
• Loss: $L_{KG} = \sum_{(h,r,t,t’)∈\mathcal{T}}−\lnσ(g(h, r , t’) − g(h, r , t ))$ , where $\mathcal{T} = {(h, r , t , t’)|(h, r , t ) ∈ \mathcal{G}, (h, r , t’) \notin \mathcal{G}}$

3.2. Attentive Embedding Propagation Layers

• GCN에서 high-order connectivity에 따라 반복적으로 emeddings를 propagate하는 방법과, GAT에서 attentive weights를 사용해서 importance를 찾아내는 방법을 동시에 고려
• single layer는 information propagation, knowledge-aware attention, information aggregation으로 구성됨
  • (Information Propagation) 하나의 entity는 여러 triplet에 속할 수 있음 → entity가 속해있는 triplets들의 정보를 반영하여 information propagation
    • ego-network (first-order connectivity structure)에 대해, 특정 relation을 가진 경우 tail에서 head로 얼마나 많은 정보가 전달될 수 있는지는 다음과 같이 계산
      • ego-network: 특정 node를 중심으로 그와 연결된 one-hop의 노드들로 구성된 네트워크
    • $e_{\mathcal{N_h}} = \sum_{(h,r,t )∈\mathcal{N_h}}π(h, r , t )e_t$
  • (Knowledge-aware Attention) relation-attention mechanism을 사용하여 아래와 같이 계산
    • $π(h, r , t ) = (W_r e_t )^⊤\tanh(W_r e_h + e_r )$
    • relation r 공간에서 $e_h$와 $e_t$의 거리에 따라 attention score가 결정 (더 가까운 entities 간에는 더 많은 정보를 줄 수 있도록)
    • 이후 softmax를 통해 h에 대한 모든 triplets에 대해 정규화: $π(h, r , t ) = \frac{ exp(π(h, r , t ))}{\sum_{(h,r’,t’)∈\mathcal{N}_h} exp(π(h, r’, t’))}$
    • GCN과 GraphSAGE에서 information propagation 과정에서 두 노드 사이의 관계를 discount factor을 사용하여 설명하는 것과 달리, KGAT에서는 proximity structure와 이웃 노드들의 각기 다른 중요도를 모두 고려하여 계산 수 있음.
    • 또한, GAT에서 node만 input으로 사용하는 것과 달리, KGAT에서는 relation과 node들을 모두 임베딩할 수 있음
  • (Information Aggregation) $e_h$와 $e_{\mathcal{N}h}$을 aggregate하여 entity h에 대해 새로운 representation을 생성 ($e_h^{(1)}=f(e_h, e{\mathcal{N}_h})$)
    • 1) GCN Aggregator: $f_{GCN} = LeakyReLU(W(e_h + e_{\mathcal{N}_h} ))$
    • 2) GraphSAGE Aggregator: $f_{GraphSage} = LeakyReLU(W(e_h ||e_{\mathcal{N}_h} ))$
    • 3) Bi-Interaction Aggregator: \(f_{Bi-Interaction} = LeakyReLU(W_1(e_h + e_{\mathcal{N}_h} )+ LeakyReLU(W_2(e_h ⊙ e_{\mathcal{N}_h} ))\)
• (High-order Propagation) 더 많은 propagation layer을 사용하여 high-order connectivity를 계산
  • l-th step을 반복하여 생성한 h의 representation: \(e^{(l)}_h = f(e^{(l−1)}_h , e^{(l−1)}_{\mathcal{N}_h})\)
  • l-ego network 내에서 h에 propagate된 정보까지 반영한 representation: \(e^{(l−1)}_{\mathcal{N}_h} = \sum_{(h,r,t )∈\mathcal{N}_h}π(h, r , t )e^{(l−1)}_t\)

3.3. Model Prediction

• l-th layer의 output은 u에서 시작하는 트리 구조의 형태로 message가 aggregate되므로, layer에 따라 다른 order로 정보가 전달될 수 있음. 따라서 layer-aggregation mechanism을 사용하여 각 step의 representations를 concat함
  • user의 경우 $e^∗_u = e^{(0)}_u ∥· · · ∥e^{(L)}_u$, item의 경우 $e^∗_i = e^{(0)}_i ∥· · · ∥e^{(L)}_i$

  → enrich initial embeddings by performing the embedding propagation operations, but also allow controlling the strength of propagation by adjusting L.

• matching score: \(\hat{y}(u,i)={e_u^*}^Te_i^*\)

3.4. Optimization

• BPR (Bayesian Personalized Ranking) loss
  • 많은 interaction이 있을수록 prediction score이 더 높도록 설정
  • $L_{CF}=\sum_{(u,i,j) \in O} -\ln\sigma(\hat{y}(u,i)-\hat{y}(u,j))$ , where $O = {(u, i, j)|(u, i) ∈ R^+, (u, j) ∈ R^−}$: training set, R+: positive interactions, R-: negative interactions
• Final loss: $L_{KGAT}=L_{KG}+L_{CF}+\lambda||\Theta||^2_2$ , where $Θ = {E,W_r ,∀l ∈ R,W^{(l )}_1 ,W^{(l )}_2 ,∀l ∈ {1, · · · , L}}$ (L_2 regularization to prevent overfitting)

3.4.1. Training

• We optimize $L_{KG}$ and $L_{CF}$ alternatively, where mini-batch Adam is adopted to optimize the embedding loss and the prediction loss. Adam is a widely used optimizer, which is able to adaptively control the learning rate w.r.t. the absolute value of gradient. In particular, for a batch of randomly sampled (h, r , t , t′), we update the embeddings for all nodes; hereafter, we sample a batch of (u, i, j) randomly, retrieve their representations after L steps of propagation, and then update model parameters by using the gradients of the prediction loss.

3.4.2. Time Complexity Analysis

• 1) KGE: \(O(|G_2|d^2)\)

• 2) attention: l-th layer \(O(|G|d_ld_{l−1})\)

• 3) prediction: \(O(\sum^L_{l=1}|G|d_l )\)

  → overall training complexity: \(O(|G_2 |d_2 + \sum_{l=1}^L|G|d_ld_{l−1} + |G|d_l )\)

4 Experiments

• RQ1: How does KGAT perform compared with state-of-the-art knowledge-aware recommendation methods?
• RQ2: How do different components (i.e., knowledge graph embedding, attention mechanism, and aggregator selection) affect KGAT?
• RQ3: Can KGAT provide reasonable explanations about user preferences towards items?

4.1. Dataset Description

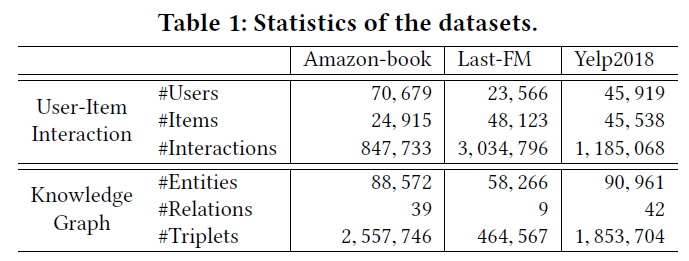
• For each dataset, we randomly select 80% of interaction history of each user to constitute the training set, and treat the remaining as the test set. From the training set, we randomly select 10% of interactions as validation set to tune hyper-parameters. For each observed user-item interaction, we treat it as a positive instance, and then conduct the negative sampling strategy to pair it with one negative item that the user did not consume before.

4.2. Experimental Settings

4.2.1. Evaluation Metrics

• Top-20, recall@20, ndcg@20

4.2.2. Baselines

• SL: FM, NFM
• regularization-based: CFKG, CKE
• path-based: MCRec, RippleNet
• graph neural network-based: GC-MC

4.2.3. Parameter Settings

• The embedding size is fixed to 64 for all models, except RippleNet 16 due to its high computational cost. We optimize all models with Adam optimizer, where the batch size is fixed at 1024. The default Xavier initializer to initialize the model parameters. We apply a grid search for hyper-parameters: the learning rate is tuned amongst {0.05, 0.01, 0.005, 0.001}, the coefficient of L2 normalization is searched in {10−5, 10−4, · · · , 101, 102}, and the dropout ratio is tuned in {0.0, 0.1, · · · , 0.8} for NFM, GC-MC, and KGAT. Besides, we employ the node dropout technique for GC-MC and KGAT, where the ratio is searched in {0.0, 0.1, · · · , 0.8}. For MCRec, we manually define several types of user-item-attributeitem meta-paths, such as user-book-author-user and user-book-genreuser for Amazon-book dataset;we set the hidden layers as suggested in [14], which is a tower structure with 512, 256, 128, 64 dimensions. For RippleNet, we set the number of hops and the memory size as 2 and 8, respectively. Moreover, early stopping strategy is performed, i.e., premature stopping if recall@20 on the validation set does not increase for 50 successive epochs. To model the third-order connectivity, we set the depth of KGAT L as three with hidden dimension 64, 32, and 16, respectively; we also report the effect of layer depth in Section 4.4.1. For each layer, we conduct the Bi-Interaction aggregator.

4.3. Performance Comparison (RQ1)

4.3.1. Overall Comparison

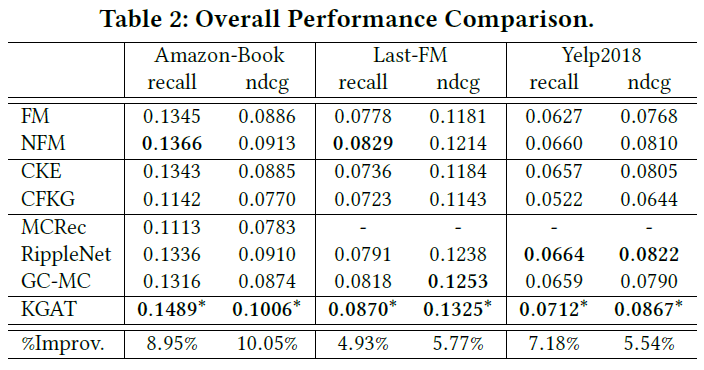
• KGAT가 모든 데이터셋에서 가장 우수한 성능을 보임
• SL methods는 CFKG, CKE보다 대부분 우수했으며, regularization-based methods가 item knowledge에 대해 많은 정보를 활용하지 못하고 있음
• FM에 비해 RippleNet에서 two-hop neighboring items를 사용하는 것이 user representations에 있어 중요함

4.3.2. Performance Comparison w.r.t. Interation Sparsity Levels

• KG를 활용하여 sparsity issue에 대처하고자 했음 → connectivity information을 활용하는 것이 issue에 대처할 수 있는지 확인
  • we divide the test set into four groups based on interaction number per user, meanwhile try to keep different groups have the same total interactions.

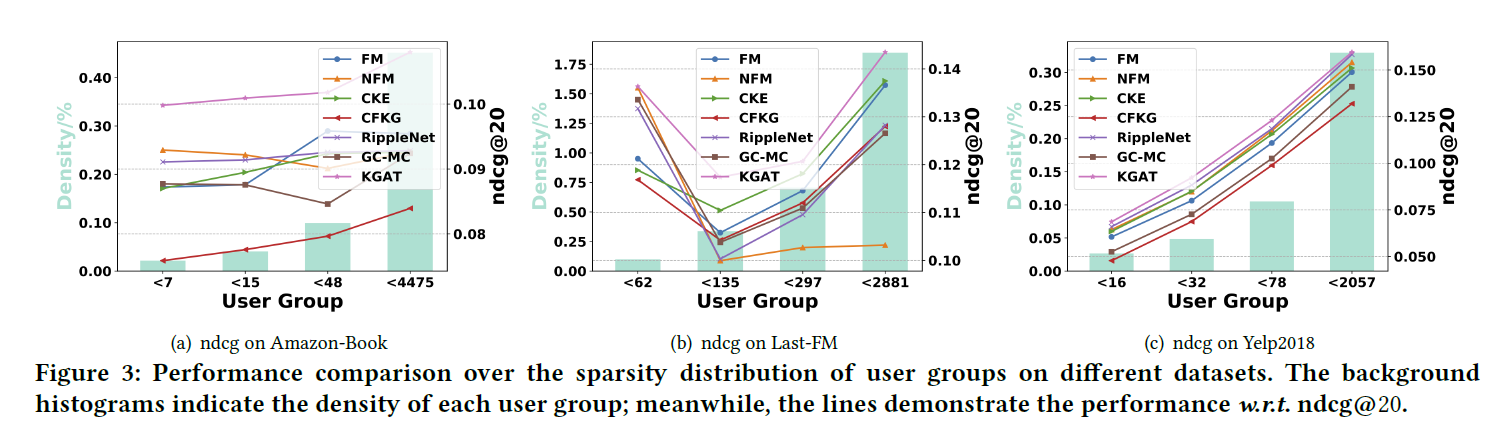
• It verifies the significance of high-order connectivity modeling, which 1) contains the lower-order connectivity used in baselines, and 2) enriches the representations of inactive users via recursive embedding propagation
• It is worthwhile pointing out that KGAT slightly outperforms some baselines in the densest user group (e.g., the < 2057 group of Yelp2018). One possible reason is that the preferences of users with too many interactions are too general to capture. High-order connectivity could introduce more noise into the user preferences, thus leading to the negative effect.

4.4. Study of KGAT (RQ2)

4.4.1. Effect of Model Depth

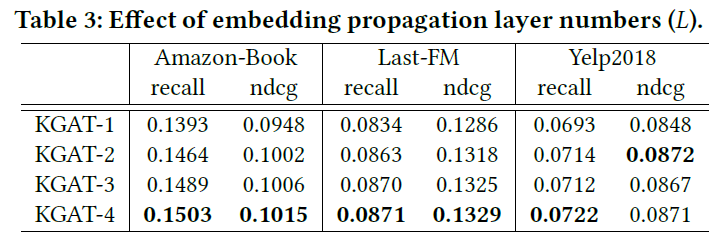
• Increasing the depth of KGAT is capable of boosting the performance substantially. Clearly, KGAT-2 and KGAT-3 achieve consistent improvement over KGAT-1 across all the board. We attribute the improvements to the effective modeling of highorder relation between users, items, and entities, which is carried by the second- and third-order connectivities, respectively.
• Further stacking one more layer over KGAT-3, we observe that KGAT-4 only achieve marginal improvements. It suggests that considering third-order relations among entities could be sufficient to capture the collaborative signal, which is consistent to the findings in [14, 33].
• Jointly analyzing Tables 2 and 3, KGAT-1 consistently outperforms other baselines in most cases. It again verifies the effectiveness of that attentive embedding propagation, empirically showing that it models the first-order relation better.

4.4.2. Effect of Aggregators

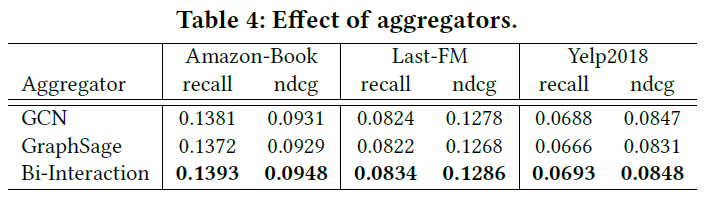
• KGAT-1_GCN is consistently superior to KGAT-1_GraphSage. One possible reason is that GraphSage forgoes the interaction between the entity representation eh and its ego-network representation e_Nh . It hence illustrates the importance of feature interaction when performing information aggregation and propagation.
• Compared to KGAT-1_GCN, the performance of KGAT-1_Bi verifies that incorporating additional feature interaction can improve the representation learning. It again illustrates the rationality and effectiveness of Bi-Interaction aggregator.

4.4.3. Effect of Knowledge Graph Embedding and Attention Mechanism

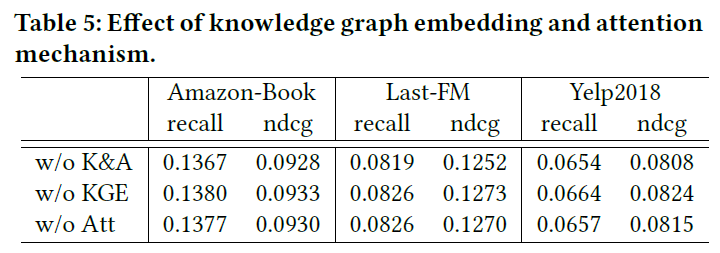
• Removing knowledge graph embedding and attention components degrades the model’s performance. KGAT-1w/o K&A consistently underperforms KGAT-1w/o KGE and KGAT-1w/o Att. It makes sense since KGATw/o K&A fails to explicitly model the representation relatedness on the granularity of triplets.
• Compared with KGAT-1w/o Att, KGAT-1w/o KGE performs better in most cases. One possible reason is that treating all neighbors equally (i.e., KGAT-1w/o Att) might introduce noises and mislead the embedding propagation process. It verifies the substantial influence of graph attention mechanism.

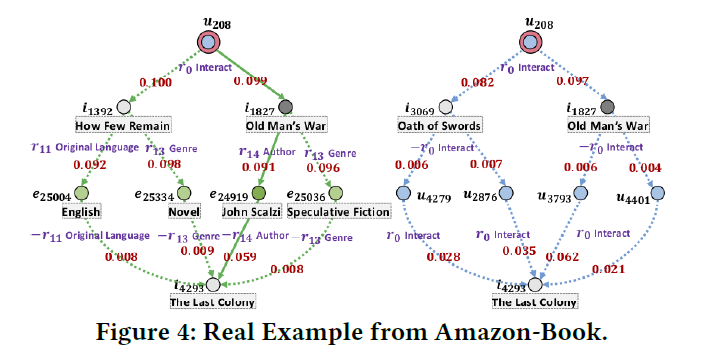
4.5. Case Study (RQ3)

5 Conclusion and Future Work

In this work, we explore high-order connectivity with semantic relations in CKG for knowledge-aware recommendation. We devised a new framework KGAT, which explicitly models the highorder connectivities in CKG in an end-to-end fashion. At it core is the attentive embedding propagation layer, which adaptively propagates the embeddings from a node’s neighbors to update the node’s representation. Extensive experiments on three real-world datasets demonstrate the rationality and effectiveness of KGAT. This work explores the potential of graph neural networks in recommendation, and represents an initial attempt to exploit structural knowledge with information propagation mechanism. Besides knowledge graph, many other structural information indeed exists in real-world scenarios, such as social networks and item contexts. For example, by integrating social network with CKG, we can investigate how social influence affects the recommendation. Another exciting direction is the integration of information propagation and decision process, which opens up research possibilities of explainable recommendation.