[논문리뷰] Modeling Relational Data with Graph Convolutional Networks (RGCN)
- 해당 논문은 GCN을 multi relation에 적용한 R-GCN을 제안하고 entity classification과 link prediction을 수행하였다.
Abstract
Knowledge graphs enable a wide variety of applications, including question answering and information retrieval. Despite the great effort invested in their creation and maintenance, even the largest (e.g., Yago, DBPedia or Wikidata) remain incomplete. We introduce Relational Graph Convolutional Networks (R-GCNs) and apply them to two standard knowledge base completion tasks: Link prediction (recovery of missing facts, i.e. subject-predicate-object triples) and entity classification (recovery of missing entity attributes). R-GCNs are related to a recent class of neural networks operating on graphs, and are developed specifically to deal with the highly multi-relational data characteristic of realistic knowledge bases. We demonstrate the effectiveness of R-GCNs as a stand-alone model for entity classification. We further show that factorization models for link prediction such as DistMult can be significantly improved by enriching them with an encoder model to accumulate evidence over multiple inference steps in the relational graph, demonstrating a large improvement of 29.8% on FB15k-237 over a decoder-only baseline.
1 Introduction
- (Background) Knowledge base는 factual knowledge를 저장하여, 다양한 task에 적용이 가능
- 그러나 incomplete한 경우가 많고, 이러한 missing information을 예측하는 것이 statistical relational learning (SRL)의 주요한 쟁점
- knowledge base를 entity가 node, triple이 labeled edge인 directed labeled multigraph로 표현
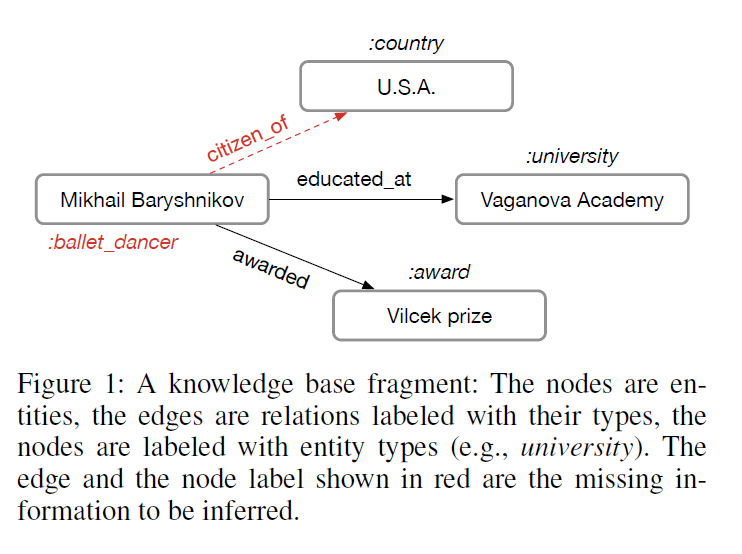
- (SRL tasks) link prediction (recovery of missing triples), entity classification (assigning types or categorical properties to entities)
- 그러나 incomplete한 경우가 많고, 이러한 missing information을 예측하는 것이 statistical relational learning (SRL)의 주요한 쟁점
- (In this study) entities에 대한 encoder model을 구축하고, 이를 SRL tasks에 적용
- entity classification: R-GCN을 통해 node representations를 구하고 softmax classifiers를 거쳐 classification을 진행 (cross-entropy loss를 통해 optimizing)
- link prediction: autoencoder와 유사 (entities에 대한 latent feature representations를 만들고 (encoder) → tensor factorization을 통해 labeled edges를 예측 (decoder))
- 연구에서는 간단하고 효과적인 factorization method - DisMult를 사용
- 이웃 정보를 사용하는 것이 missing facts를 recover하는 데 도움을 준다는 것을 확인
- (Contributions)
- 1) 처음으로 GCN을 사용하여 relational data를 모델링
- 2) parameter sharing + sparsity constraints와 관련한 technique를 도입
- 3) link prediction에서 factorization model의 성능을 향상
2 Neural relational modeling
- $G=\mathcal{(V, E, R)}$ where nodes $v_i \in \mathcal{V}$, labeled edges $(v_i, r, v_j) \in \mathcal{E}$, and relation type $r \in \mathcal{R}$
2.1 Relational graph convolutional networks
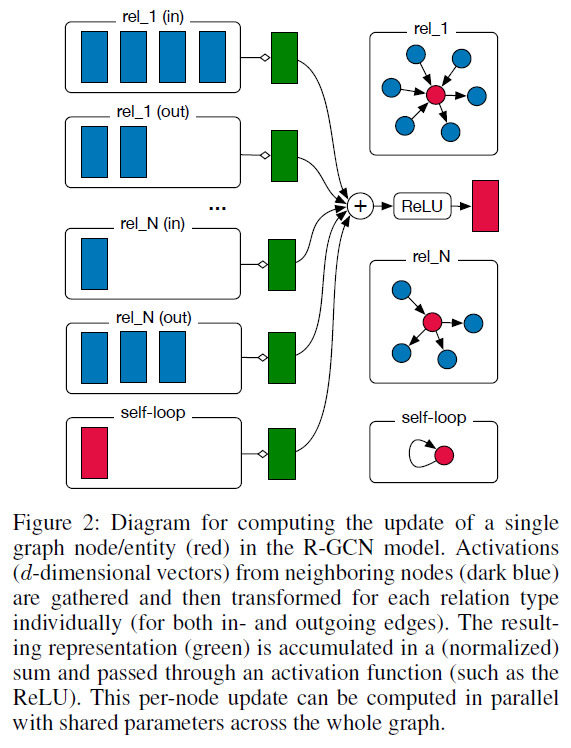
- local graph neighborhoods의 정보를 활용하는 GCN을 large-scale relational data로 확장
- (GCN) 미분 가능한 message-passing framework: $h_i^{(l+1)}=\sigma(\sum_{m \in \mathcal{M}_i}g_m(h_i^{(l)}, h_j^{(l)}))$
- $h_i^{(l)} \in \mathbb{R}^{d^{(l)}}$: node $v_i$의 l번째 layer의 hidden state ($d^{(l)}$: layer’s representations의 차원)
- $g_m(\cdot, \cdot)$: incoming messages의 형태 (linear transformation - $g_m(h_i^{(l)}, h_j^{(l)})=Wh_j$ 등)
- $\mathcal{M}_i$: node $v_i$의 incoming message set
- (In this study) relational multi-graph에서 node의 forward-pass update를 계산하는 simple propagation model
- linear transformation인 경우, $h_i^{(l+1)}=\sigma(\sum_{r \in \mathcal{R}}\sum_{j \in \mathcal{N}i^r}\frac{1}{c{i,r}}W_r^{(l)}h_j^{(l)}+ W_0^{(l)}h_i^{(l)})$
- $\mathcal{N}_i^r$: relation r에 대한 node의 neighobor indices의 set
- $c_{i,r}$: normalization constant (학습될 수도 있고, 사전에 정의할 수도 있음. e.g. $|\mathcal{N}_i^r|$)
- 기존의 GCN과 달리, relation-specific한 transformation($c_{i,r}$)을 거침
- 이전 시점(layer)에서 자신의 영향을 반영하기 위해 self-connection($W_0^{(l)}h_i^{(l)}$)을 추가
- sparse matrix multiplication으로 효율적으로 계산 가능 (explicit summation없이 계산 가능)
- 여러 relational steps에 대한 dependencies를 반영하기 위해 레이어들을 쌓아서 진행
- linear transformation인 경우, $h_i^{(l+1)}=\sigma(\sum_{r \in \mathcal{R}}\sum_{j \in \mathcal{N}i^r}\frac{1}{c{i,r}}W_r^{(l)}h_j^{(l)}+ W_0^{(l)}h_i^{(l)})$
2.2 Regularization
- 위의 식을 계산하려면, relation type이 많아질 수록, 데이터가 적은 relations에 대해 overfitting이 발생할 수 있고 모델의 사이즈가 매우 커질 수 있음
- 주어진 적은 양의 relation으로만 학습하기 때문으로 보임
- 이를 보완하기 위해 두 가지 regularizing methods를 사용: 1) basis decomposition, and 2) block-diagonal decomposition
- Basis decomposition: $W_r^{(l)}=\sum^B_{b=1}a_{rb}^{(l)}V_b^{(l)}$
- basis transformation $V_b^{(l)} \in \mathbb{R}^{d^{(l+1)} \times d^{(1)}}$과 coefficients $a_{rb}^{(l)}$의 linear combination
- basis transformation은 relation과 상관없이 share → weight sharing
- rare한 relations와 frequent relations 간 parameter updates를 공유하기 때문에 오버피팅을 방지할 수 있음
- rare한 relations에 대해서도 다른 relation의 정보를 통해 좀 alleviate할 수 있는 것으로 보임
- Block-diagonal decomposition: $W_r^{(l)}=\oplus_{b=1}^BQ_{br}^{(l)}$
- rare한 relations에 대해서도 다른 relation의 정보를 통해 좀 alleviate할 수 있는 것으로 보임
- $Q_{br}^{(l)} \in \mathbb{R}^{(d^{(l+1)/B} \times d^{(l)/B})}$ → $W_r^{(l)}$: block-diagonal matrices ($diag(Q_{1r}^{(l)}, … , Q_{Br}^{(l)}$)
- relation마다 다른 weight matrices → sparsity constraint
- latent features는 within group끼리 더 tightly coupled되도록 설계
→ decompositions를 통해 highly multi-relational data를 더 적은 파라미터로 학습할 수 있게 됨
Overall R-GCN model
- L개의 layers를 쌓은 후, 각 layer의 output이 다음 layer의 input으로 들어감
- 첫번째 layer의 경우, 각 노드별로 features가 지정되지 않는 경우 unique한 원핫 벡터를 사용
- block representation을 할 때는, 원핫 벡터를 single linear transformation을 통해 dense representation 수행
- pre-defined feature vectors를 노드의 초기 representation으로 사용할 수도 있음
3 Entity classification
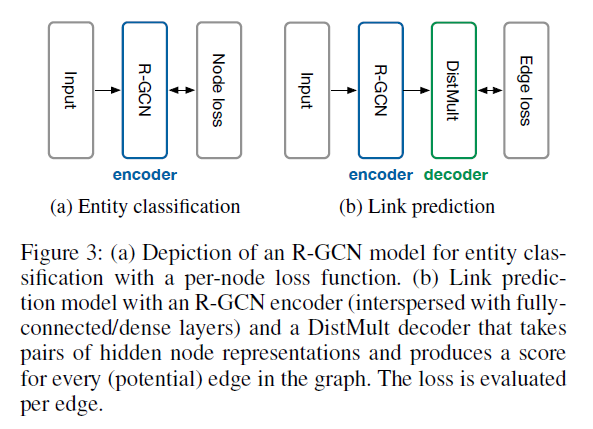
- R-GCN layers를 쌓은 후, 마지막 layer의 output에 softmax activation function을 적용
- (loss) cross-entropy (unlabeled node에 대해서는 loss를 계산하지 않음): $\mathcal{L}=-\sum_{i\in\mathcal{Y}}\sum^K_{k=1}t_{ik}\ln h_{ik}^{(L)}$
- $\mathcal{Y}$: label이 있는 노드들의 set
- $h_{ik}^{(L)}$: i번째 node의 k번째 entry of network output
- $t_{ik}$: ground truth label
- full-batch gradient descent
4 Link prediction
- entity encoder와 scorig function (decoder)로 구성된 graph auto-encoder 모델을 도입
- (encoder) entity ($v_i \in \mathcal{V}$)를 real-valued vector ($e_i \in \mathbb{R}^d$)로 인코딩
- (decoder) entity representation에 맞춰 edge를 표현 → triple (subject, relation, object)의 score을 메김 ($s:\mathbb{R}^d\times\mathcal{R}\times\mathbb{R}^d → \mathbb{R}$)
- tensor/neural factorization model을 사용한 link prediction 방법들을 모두 활용 가능
- 기존 link prediction 연구들에서는 entities를 하나의 실수 벡터로 표현했던 것과 달리, encoder을 도입하여 L개의 hodden layer를 거친 output을 사용
- (DistMult) 해당 연구에서는 DistMult factorization을 scoring function으로 사용
-
모든 relation r은 diagonal matrix $R_r \in \mathbb{R}^{d\times d}$과 관련이 있으며, triple은 다음과 같이 scored: $f(s,r,o)=e_s^TR_re_o$

DisMult, ComplEx, RESCAL, … : factorization model
-
- (training) negative sampling을 진행하고 cross-entropy loss를 사용하여 모델을 train
-
\[\mathcal{L}=-\frac{1}{(1+\omega)|\hat{\mathcal{E}}|}\sum_{(s,r,o,y)\in\mathcal{T}}y \log l(f(s,r,o))+(1-y)\log (1-l(f(s,r,o)))\]
- $\omega$: negative sample 수, $\mathcal{T}$: real/corrupted triples의 전체 set, $l$: sigmoid function, $y$: negative triples인 경우 0 positive인 경우 1
-
\[\mathcal{L}=-\frac{1}{(1+\omega)|\hat{\mathcal{E}}|}\sum_{(s,r,o,y)\in\mathcal{T}}y \log l(f(s,r,o))+(1-y)\log (1-l(f(s,r,o)))\]
5 Empirical evaluation
5.1 Entity classification experiments
-
(Datasets) four datasets in Resource Description Framework (RDF) format: AIFB, MUTAG, BGS, and AM
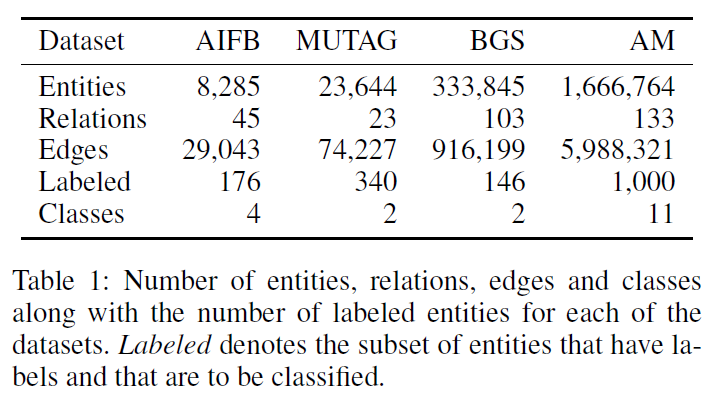
- Relations in these datasets need not necessarily encode directed subject-object relations, but are also used to encode the presence, or absence, of a specific feature for a given entity.
- In each dataset, the targets to be classified are properties of a group of entities represented as nodes.
- We remove relations that were used to create entity labels: employs and affiliation for AIFB, isMutagenic for MUTAG, hasLithogenesis for BGS, and objectCategory and material for AM.
- (Baselines) recent state-of-the-art classification results from 1) RDF2Vec embeddings (Ristoski and Paulheim 2016), 2) Weisfeiler-Lehman kernels (WL) (Shervashidze et al. 2011; de Vries and de Rooij 2015), and 3) hand-designed feature extractors (Feat) (Paulheim and F¨umkranz 2012).
- Feat assembles a feature vector from the in- and out-degree (per relation) of every labeled entity.
- RDF2Vec extracts walks on labeled graphs which are then processed using the Skipgram (Mikolov et al. 2013) model to generate entity embeddings, used for subsequent classification.
- All entity classification experiments were run on CPU nodes with 64GB of memory.
-
(Results) training set 중에서 20%는 validation set으로 사용
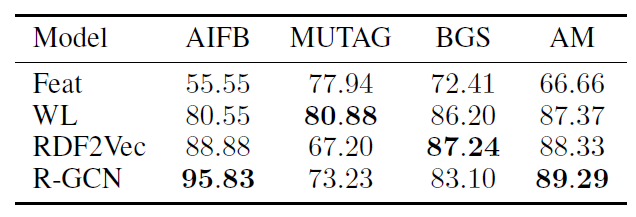
- R-GCN: 2-layer model with 16 hidden unitsm bsis function decomposition, Adam for 50 epochs (lr=0.01), normalization constant: $|\mathcal{N}_i^r|$
- MUTAG data의 경우 molecular graphs로 이루어져 있고, BGS의 경우 hierarchical feature descriptions가 주어진 rock types에 대한 dataset
- labeled entities는 특정 feature을 인코딩하는 high-degree hub nodes를 통해서만 연결되어 있음
- 따라서 attention을 도입하여 중요한 노드에 더 큰 가중치를 부여하도록 하여 해결할 수 있을 것이라 봄 (normalization constant를 $\frac{1}{c_{i,r}}$로 설정하고 data-dependent attention weights $a_{i,j,r}$을 사용)
5.2 Link prediction experiments
- (Datasets) 1) FB15k, a subset of the relational database Freebase, and 2) WN18, a subset of WordNet containing lexical relations between words.
- Toutanova and Chen (2015)에 따르면, 두 데이터셋을 그대로 사용하기엔 심각한 flaw가 존재함
- $t$가 training set, $t’$가 test set일 때 inverse triplet pairs $t = (e_1, r, e_2)$ and $t’ = (e_2, r^{-1}, e_1)$가 존재할 수 있음 → triple pairs의 prediction task의 많은 부분을 memorization task처럼 작동할 수 있음
- 따라서 이러한 inverse triplet pairs를 제거한 FB15k-237를 추가로 evaluate하였음
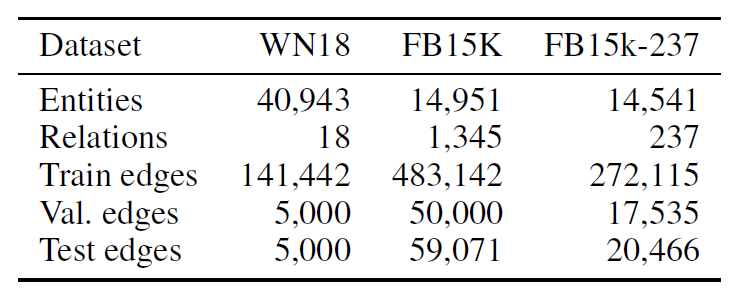
- Toutanova and Chen (2015)에 따르면, 두 데이터셋을 그대로 사용하기엔 심각한 flaw가 존재함
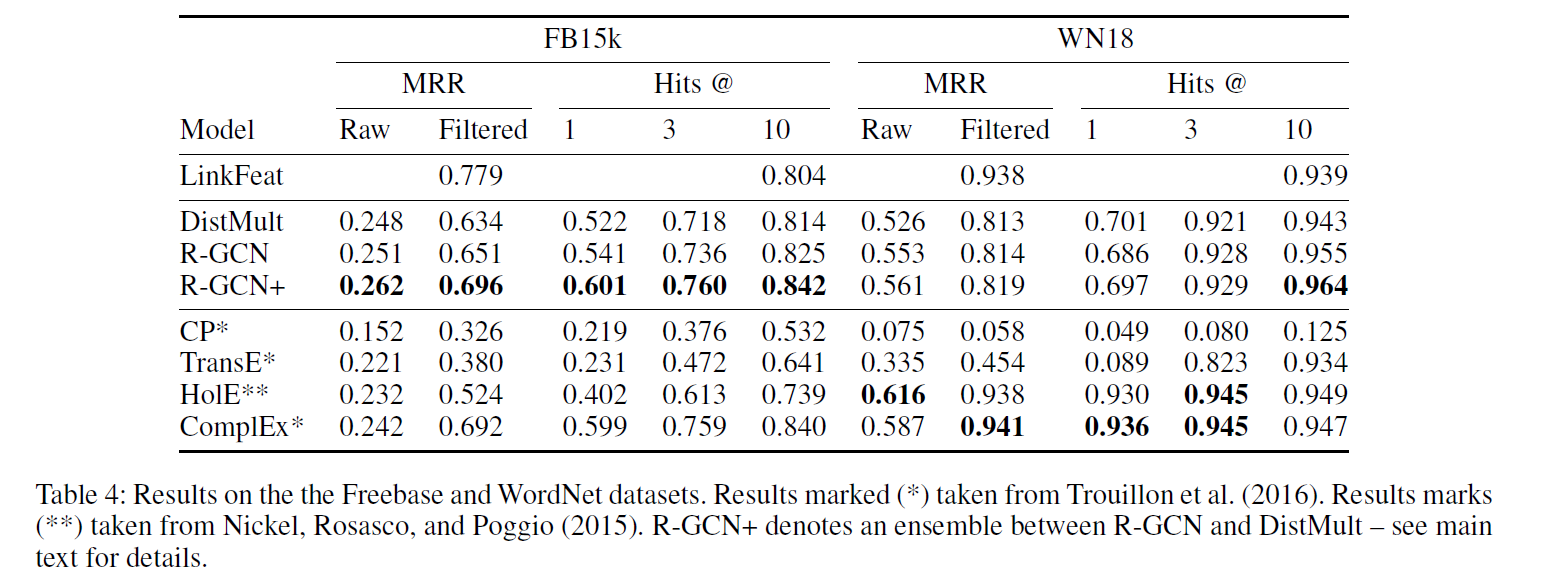
- (Baselines) ComplEx facilitates modeling of asymmetric relations by generalizing DistMult to the complex domain, while HolE replaces the vector-matrix product with circular correlation. Finally, we include comparisons with two classic algorithms – CP (Hitchcock 1927) and TransE (Bordes et al. 2013).
- (Results) mean reciprocal rank (MRR) and Hits at n (H@n)
- We found a normalization constant defined as \(c_{i,r}=c_i=\sum_r |\mathcal{n}_i^r|\) – in other words, applied across relation types – to work best.
- For FB15k and WN18, we report results using basis decomposition with two basis functions, and a single encoding layer with 200-dimensional embeddings.
- For FB15k-237, we found block decomposition to perform best, using two layers with block dimension 5*5 and 500-dimensional embeddings.
- We regularize the encoder through edge dropout applied before normalization, with dropout rate 0.2 for self-loops and 0.4 for other edges. Using edge droupout makes our training objective similar to that of denoising autoencoders (Vincent et al. 2008). We apply l2 regularization to the decoder with a penalty of 0.01.
- We use the Adam optimizer (Kingma and Ba 2014) with a learning rate of 0.01. For the baseline and the other factorizations, we found the parameters from Trouillon et al. (2016) – apart from the dimensionality on FB15k-237 – to work best, though to make the systems comparable we maintain the same number of negative samples (i.e. $\omega$ = 1). We use full-batch optimization for both the baselines and our model.
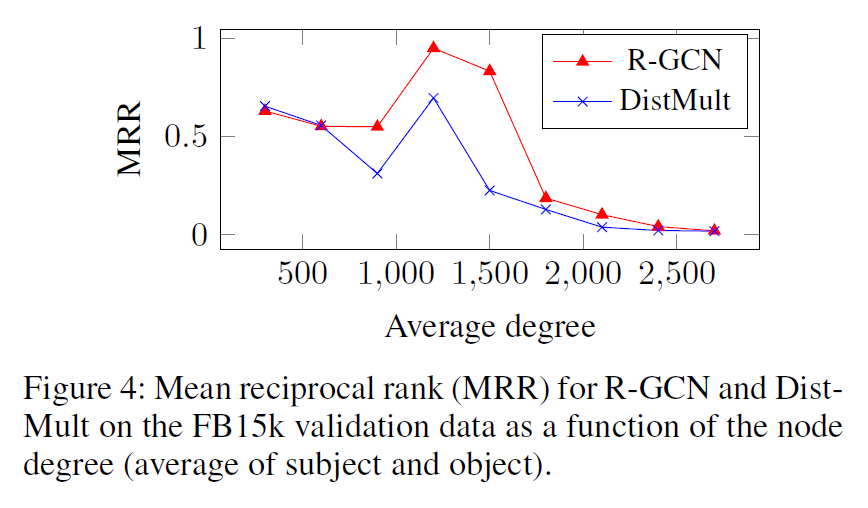
- It can be seen that our model performs better for nodes with high degree where contextual information is abundant.
- The observation that the two models are complementary suggests combining the strengths of both into a single model, which we refer to
as R-GCN+.
- On FB15k and WN18 where local and long distance information can both provide strong solutions, we expect R-GCN+ to outperform each individual model.
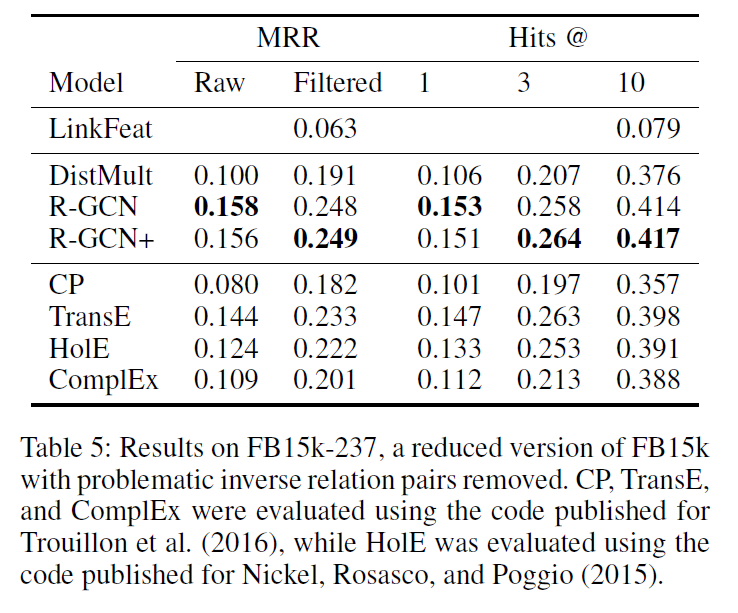
- This suggests that combining the R-GCN encoder with the ComplEx scoring function (decoder) may be a promising direction for future work.
- we show results for FB15k-237 where (as previously discussed) inverse relation pairs have been removed and the LinkFeat baseline fails to generalize.
6 Related Work
6.1 Relational modeling
- (Factorization based knowledge bases) DistMult (Yang et al. 2014): a special and simpler case of the RESCAL factorization (Nickel, Tresp, and Kriegel 2011), more effective than the original RESCAL in the context of multi-relational knowledge bases.
- Many of these factorization-based approaches can be regarded as modifications or special cases of classic tensor decomposition methods such as CP or Tucker.
- (Incorporation of paths) Incorporation of paths between entities in knowledge bases has recently received considerable attention.
- We can roughly classify previous work into (1) methods creating
auxiliary triples, which are then added to the learning objective
of a factorization model (Guu, Miller, and Liang 2015; Garcia-Duran, Bordes, and Usunier 2015)
- largely orthogonal to ours, as we would also expect improvements from adding similar terms to ourloss (in other words, extending our decoder).
- (2) approaches using paths (or walks) as features when predicting edges
(Lin et al. 2015)
- more comparable than (1): R-GCNs provide a computationally cheaper alternative to these path-based models.
- (3) doing both at the same time (Neelakantan, Roth, and McCallum 2015; Toutanova et al. 2016).
- Direct comparison is somewhat complicated as path-based methods used different datasets (e.g., sub-sampled sets of walks from a knowledge base).
- We can roughly classify previous work into (1) methods creating
auxiliary triples, which are then added to the learning objective
of a factorization model (Guu, Miller, and Liang 2015; Garcia-Duran, Bordes, and Usunier 2015)
6.2 Neural networks on graphs
- (GCNs) R-GCn primarily motivated as an adaption of previous work on GCNs
(Bruna et al. 2014; Duvenaud et al. 2015; Defferrard, Bresson, and Vandergheynst 2016; Kipf and Welling 2017) for large-scale and highly multi-relational data, characteristic of realistic knowledge bases.
- A number of extensions to the original graph neural network have been proposed, most notably (Li et al. 2016) and (Pham et al. 2017), both of which utilize gating mechanisms to facilitate optimization.
- R-GCNs can further be seen as a sub-class of message passing neural networks (Gilmer et al. 2017), which encompass a number of previous neural models for graphs, including GCNs, under a differentiable message passing interpretation.
7 Conclusions
- We have introduced relational graph convolutional networks (R-GCNs) and demonstrated their effectiveness in the context of two standard statistical relation modeling problems: link prediction and entity classification.
- For the entity classification problem, we have demonstrated that the R-GCN model can act as a competitive, end-to-end trainable graph-based encoder.
- For link prediction, the R-GCN model with DistMult factorization as the decoding component outperformed direct optimization of the factorization model, and achieved competitive results on standard link prediction benchmarks.
- Enriching the factorization model with an RGCN encoder proved especially valuable for the challenging FB15k-237 dataset, yielding a 29.8% improvement over the decoder-only baseline.
- There are several ways in which our work could be extended.
- For example, the graph auto-encoder model could be considered in combination with other factorization models, such as ComplEx (Trouillon et al. 2016), which can be better suited for modeling asymmetric relations.
- It is also straightforward to integrate entity features in R-GCNs, which would be beneficial both for link prediction and entity classification problems.
- To address the scalability of our method, it would be worthwhile to explore subsampling techniques, such as in Hamilton, Ying, and Leskovec (2017).
- Lastly, it would be promising to replace the current form of summation over neighboring nodes and relation types with a data-dependent attention mechanism. Beyond modeling knowledge bases, R-GCNs can be generalized to other applications where relation factorization models have been shown effective (e.g. relation extraction).

댓글남기기